
Moreover, through examples topic is explained and for the detailed explanation, their applications are also discussed. In this article, the basic definition of limit its formula, and different methods are discussed which helps to evaluate the limits of different functions.

The Limit Laws Assumptions: c (x) and limg(x)exist Direct Substitution Property: If f is a polynomial or rational function and a is in the domain of f,then limf(x) a Simpler Function Property: If f (x)g(x) when limit exists. Limit is a value that a function (or sequence) approaches as the input (or index) approaches some value” Formula: The Limit Laws Math131 Calculus I The Limit Laws Notes 2.3 I. In this article, the basic definition of limit its formula, and detailed with the help of examples will be discussed easily. Learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. Learn how we define the derivative using limits. Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. There are two further types to categorize the integrals indefinite and definite integrals limits are defined and while indefinite integrals limits are not shown. The derivative of a function describes the function's instantaneous rate of change at a certain point. Example: (x2 1) (x 1) Lets work it out for x1: (12 1) (1 1) (1 1) (1 1) 0 0 Now 0/0 is a difficulty We dont really know the value of 0/0 (it is 'indeterminate'), so we need another way of answering this. This product is protected by copyright and distributed under licenses restricting its use, copying, distribution, and decompilation.The notion of limit in topology is more extensive and relates to the concepts of direct limit and limit in theory. © Maplesoft, a division of Waterloo Maple Inc., 2023. The limit of f(x), as x approaches c, is L, denoted by lim x cf(x) L, means that given any > 0, there exists > 0 such that for all x c, if x c <, then f(x) L <. Plots:-display(p||(1.9), view=,tickmarks=,],labels=) įigure 1.2.2 Schematic for Definition 2.1 Definition 1: The Limit of a Function f Let I be an open interval containing c, and let f be a function defined on I, except possibly at c. The Formal Definition of the Limit limxc-f(x) L to denote the limit of f(x) as x approaches c from the left is L limxc+f(x) L to denote the limit. P8:=plottools:-arrow(,Vector().01.1.1,double_arrow): A.1 Proof of Various Limit Properties A.2 Proof of Various Derivative Properties A.3 Proof of Trig Limits A.4 Proofs of Derivative Applications Facts A. P7:=plottools:-polygon(,],color=yellow,transparency=.8): If and only if for every &varepsilon > 0 there exists a number &delta > 0 with the property that if 0 The limit of f x as x approaches a is the number L, that is But also keep in mind that it took nearly 100 years for the mathematics community to settle on this form of the statement of what "near" should mean. The notation for the "limit of f x as x approaches a " isĪs Definition 1.2.1 is read, keep in mind that all it is trying to say is that for x "near" a, the values of f x are "near" L. The limit is a number designated by the letter L. The section concludes with a more precise definition of one-sided limits first seen in Section 1.1.ĭefinition 1.2.1 is a precise definition of the limit of the real-valued function f x. The strictest definition of a limit is as follows: Say A is a series.

Next, the algebraic manipulations involved in applying the precise definition will be explored for four examples. The first step is to develop a graphical interpretation of the precise definition. This section gives a formal definition of the limit, one that provides a framework upon which a wide range of useful techniques will be developed. The development of general tools for working with and applying limits requires a more precise definition of limit. Example 1: The Limit Exists Whether x approaches a from the left or from the right, the function approaches L. In fact, the statement lim x → a f x = L means the difference between f x and L can be made as small as desired for all values of x sufficiently close to - but different from - a. This intuition was captured in an informal definition.
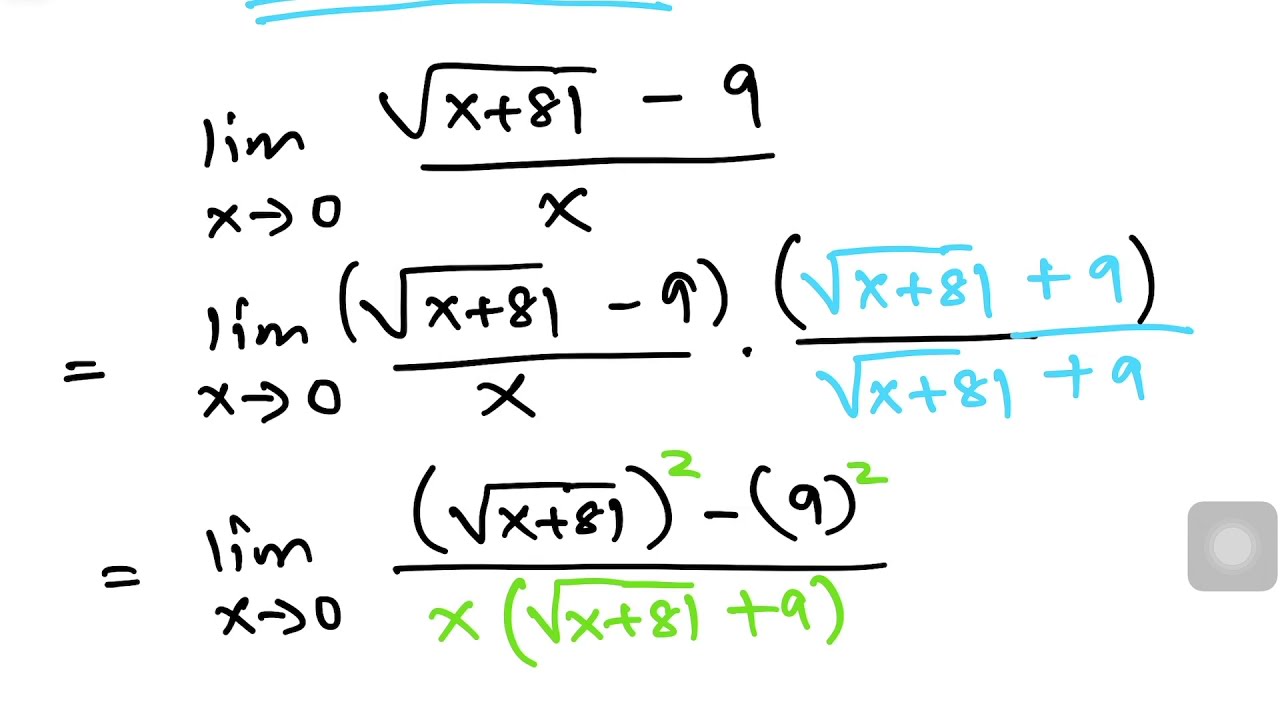
Section 1.1 provided an intuitive introduction to the notion of a mathematical limit. Section 1.2: Precise Definition of a Limit


 0 kommentar(er)
0 kommentar(er)
